티스토리 뷰
이번 포스팅의 주제인 이분 매칭 문제는 네트워크 플로우 연장선에 있는 문제입니다.
2020/09/09 - [알고리즘] - 포드 풀커슨 알고리즘
우선, 이분 매칭을 공부하기 위해선 이분 그래프라는 것을 알 필요가 있습니다.
이분 그래프란 두 집합으로 나뉜 그래프의 정점들의 간선이 상대 집합에 속한 정점으로 연결된 그래프입니다.
성별이나, 주종관계, 사람과 작업 등의 관계가 주어진다면 이를 이분 그래프로 표현할 수 있습니다.

여기서 이분 그래프의 각 요소들을 문제의 조건에 맞춰 대응시키는 것이 이분 매칭 문제입니다.
이런 이분 매칭 문제는 앞서 소개한 네트워크 플로우를 이용하면 쉽게 풀 수 있습니다.
이분 그래프의 각 간선을, 연결되지 않은 것(0) 과 연결된 것(1) 인 용량이 1인 간선으로 고려할 수 있기 때문입니다.

이분 그래프의 양쪽에 소스와 싱크를 생성하고 두개로 나눠진 집합을 각각 소스와 싱크에 연결합니다.
여기서 네트워크 플로우의 최대 유량을 계산하면 이분 그래프의 최대 매칭을 알 수 있습니다.
이분 매칭 알고리즘의 시간 복잡도
이분 매칭은 포드-풀커슨 알고리즘에서 소개한 소스코드로 구현을 해도 상관없습니다.
BFS 로 구현할 때의 시간 복잡도는 O(|V||E|^2) 이고 DFS 로 구현할 떄의 시간 복잡도는 O(|E|f) 였습니다.
이분 매칭에서는 최대 유량이 O(|V|) 이기 때문에 DFS 로 구현하면 시간 복잡도는 O(|E||V|) 가 됩니다.
O(|E||V|) 로 구현하는 것이 O(|V||E|^2) 로 구현하는 것 보다 낫기 때문에 이번 포스팅에서는 DFS 로 구현할 것입니다.

먼저, 연결가능한 간선들을 입력받습니다.
1번 정점부터 매칭 가능한 정점들을 정점에 연결된 순서대로 찾아볼 것입니다.

4번 정점이 아직 누구에게도 연결되지 않은 상태이기 때문에 1번 정점과 4번 정점이 연결되었습니다.

2번 정점에서 연결가능한 정점을 찾아봅니다.
이미 4번 정점은 1번 정점에게 연결된 상태이지만 2번 정점은 매칭될 수 있는 다른 정점이 없습니다.
따라서 1번 정점이 다른 정점과 연결될 수 있는지 확인을 해봐야 합니다.
1번이 5번과 연결될 수 있기 때문에 1번과 4번의 연결을 끊고, 1번과 5번을 연결하고, 2번은 4번과 연결될 수 있습니다.

3번 정점을 살펴봅니다.
3번 정점은 5번 정점과만 연결될 수 있기 때문에 1번 정점이 다시 다른 정점과 연결될 수 있는지 확인해야 합니다.
4번은 이미 2번이 점유하고 있고, 2번은 다른 정점과 연결될 수 없기 때문에 2번과 4번의 연결을 끊을 순 없습니다.
1번이 6번과 연결될 수 있기 때문에 1번과 5번의 연결을 끊고, 1번과 6번을 연결하고, 3번은 5번과 연결될 수 있습니다.
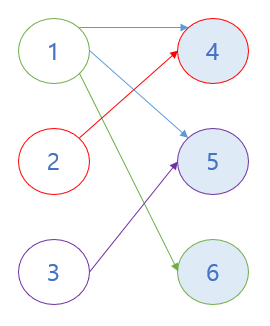
왼쪽의 모든 정점을 오른쪽 정점에 성공적으로 매칭시킨 모습입니다.
이제 소스코드로 구현해보겠습니다.
int L,R;
//왼쪽, 오른쪽 정점의 개수입니다.
bool adj[left_max][right_max];
//각 정점이 어느 정점에 연결될 수 있는지 저장할 배열입니다.
vector<int> leftmatch,rightmatch;
//각 정점이 연결된 정점의 번호를 저장할 벡터입니다.
vector<bool> visited;
//
bool dfs(int l) {
if(visited[l]) return false;
//이미 방문했던 노드라면 방문할 필요가 없습니다.
visited[l]=true;
//
for(int r=0;r<R;r++){
//L과 매칭할 오른족 정점을 찾아봅니다.
if(adj[l][r]){
//L과 R이 만날 경로가 존재한다면 더 확인해볼 가치가 있습니다.
if(rightmatch[r]==-1 || dfs(rightmatch[r])){
//R이 아직 누구와도 연결되지 않았거나,
leftmatch[l]=r; rightmatch[r]=l; return true;
//서로 매칭을 시키고, 새로운 매칭이 되었음을 반환합니다.
}
}
}
return false;
//오른쪽 정점을 모두 탐색했음에도 연결을 못했다면 매칭 실패를 반환합니다.
}
int match(){
leftmatch=vector<int>(L,-1); rightmatch=vector<int>(R,-1);
//각 정점은 초기에 누구와도 연결되어있지 않습니다.
int size=0;
//최대 연결 개수를 저장합니다.
for(int l=0;l<L;l++){
//왼쪽 정점을 순차적으로 체크합니다.
visited=vector<bool>(L,false);
//
if(dfs(l)) size++;
//새로운 연결에 성공했다면 최대 연결 개수를 증가시킵니다.
}
return size;
//최대 연결 개수를 반환합니다.
}
연습문제
2020/09/12 - [백준] - 백준 소스코드 [C++] 2188 축사 배정
네트워크 플로우를 활용한 이분 매칭에 대한 포스팅이었습니다.
오타 지적과 조언은 언제나 환영입니다.
'알고리즘' 카테고리의 다른 글
| 트라이 (0) | 2021.03.14 |
|---|---|
| 컨벡스 헐 알고리즘 (0) | 2020.10.16 |
| 포드 풀커슨 알고리즘 (0) | 2020.09.09 |
| 플로이드 와샬 알고리즘 (0) | 2020.09.09 |
| SPFA (Shortest Path Faster Algorithm) (0) | 2020.09.07 |
- Total
- Today
- Yesterday
- Testable
- WWDC21
- WWDC19
- 다익스트라 시간복잡도
- 포드 풀커슨 알고리즘
- 벨만포드 알고리즘
- 최단경로 문제
- WWDC16
- 벨만포드 시간복잡도
- mach-o
- State Restoration
- WWDC17
- 부스트캠프 6기
- IOS
- 네트워크 플로우
- 최단경로 알고리즘
- observeOn
- 컴퓨터 추상화
- 최대 매칭
- 강한 순환 참조
- 최단경로문제
- MeTal
- rxswift
- CompositionalLayout
- test coverage
- 코딩대회
- CPU와 Memory
- 에드몬드 카프 알고리즘
- HIG
- 네트워크 유량
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
